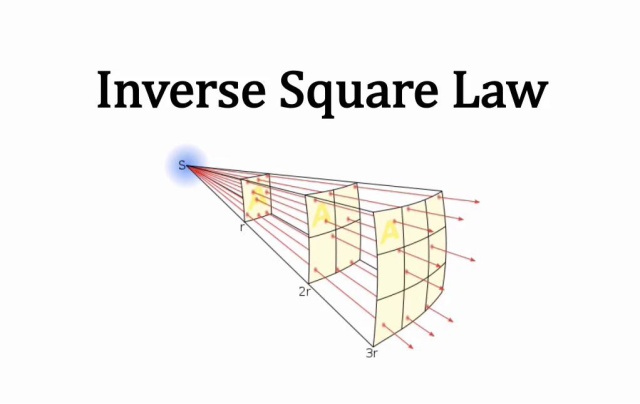
If you asked what skills someone in cinematography should have, the understanding of a certain equation in physics probably wouldn’t be anyone’s first answer, if thought of as an answer in the first place. Nevertheless, it actually would be useful, specifically for someone in charge of lighting or sound. This equation is the Inverse Square Law.
The Inverse Square Law states that the intensity of a physical quantity is inversely proportional to the square of its distance. In the context of lighting, we use it to calculate the falloff of light. It’s not as complicated as it sounds. If you want to simplify it, just do what I do and think like a caveman to understand the gist of it: Light close. Light strong. Light far. Light weak.
It can be expressed in this equation: 𝑖 = 1/𝑑2
Knowing the inverse square law is a great way to keep lighting relatively consistent in a controlled environment without having to use a light meter. Let’s apply the equation in a real life scenario. Imagine you are lighting a subject from 1 metre away. We can use that as our benchmark of 100% light intensity.
If we move the light two metres away we are doubling the distance, we can use the equation to figure out how much weaker the light becomes.
𝑖 = 1/22
𝑖 = 1/4
Moving the light two metres from its original position makes the new intensity of the light 25% of the light when it was just one metre away.
You might notice that the falloff gets less drastic when the light gets even further away. This mathematically shows that lighting a subject can be done more evenly when you light them from further away. You can see this in practice if you take two pictures with identical setups minus the light’s distance. The one with the closer light would produce a much stronger shadow than the one with the further light, as seen here.
Taking this example to the extreme shows why sunlight lighting is hard to replicate— the sun is very far away from what it lights up on earth. The equation also can be used in reverse to figure out how intense the light gets when we bring it closer instead. If we halve the distance from the subject and put it 0.5 metres away, the light quadruples in intensity.
𝑖 = 1/0. 52
𝑖 = 1/0. 25
𝑖 = 4
The inverse square law also applies to sound, but it works a bit different than what you would think. You find the intensity of a sound with the inverse square law, but our ears and our microphones measure sound through pressure change. You use the inverse distance law to find that. At the end of the day, the inverse square law just restates a fact that everyone knows, but understanding it would do good for anyone working with lighting. If this blog had too much math for you, then I could at least give you this as your take away:
Light close. Light strong. Light far. Light weak.